Rubik's Cube: tutoriel facile pour débutant en 6 étapes

J'ai appris à résoudre un Rubik's cube il y à deux jours alors croyez moi il n'y à rien de très compliqué et je compte bien vous en persuader. Oh bien sûr vous allez devoir faire travailler votre cerveau mais en sois c'est plutôt une bonne chose. Je suis bien évidemment passé par différents sites proposant des tutoriels mais très souvent je me suis trouvé confronté à des cas de figure totalement ignorés ou des explications insuffisantes. J'ai donc pris l'initiative de rédiger mon propre tutoriel et d'y faire figurer toutes les informations qui m'on manquées lors de mon apprentissage. J'ai également pris la liberté de ne pas utiliser de notation (vous savez les choses comme RFL'DF'L2) car, bien qu'intéressantes à connaitre, elles sont selon moi une surcharge à ce stade de l'initiation. J'espère donc que vous prendrez plaisir à lire ces quelques paragraphes et qu'au final vous trouverez ce tutoriel pour débutant, simple et bien expliqué.

• Rubik's Cube: tutoriel facile pour débutant en 6 étapes
  • Faire connaissance avec Rubik avant de mettre la main au cube
    • Les différents blocs
    • Le code couleur
  • Première étape: placer les arêtes et former la croix
  • Deuxième étape: placer les coins pour former la face noire et sa couronne
  • Troisième étape: construire la seconde couronne grâce à Mme Tetenlair
    • Pivoter une arête de 45° pour la placer à droite
    • Pivoter une arête de 45° pour la placer à gauche
  • Quatrième étape: la croix jaune
    • Algorithmes de la virgule et de la barre
  • Cinquième étape: La croix bien orientée, algorithmes de la chaise
    • Déplacer trois arête dans le sens horaire (chaise de droite)
    • Déplacer trois arête dans le sens antihoraire (chaise de gauche)
    • Conclusion sur les algorithmes de la chaise
  • Sixième étape: Finir le cube
    • Déplacer les coins avec l'algorithme du petit canard curieux
      • Déplacer trois coins dans le sens horaire
      • Déplacer trois coins dans le sens antihoraire
    • Bien orienter les arêtes avec l'algorithme de la double chaise
  • Conclusion
  • BONUS: Pivoter une arête bien placée mais mal orientée
    • L'algorithme de la nouvelle pair de chaussures.
  • BONUS: Pivoter deux coins bien placée mais mal orientée
    • Algorithme de Fab et mnémotechnique du courant d'air
    • Astuce

Faire connaissance avec Rubik avant de mettre la main au cube

Avant d'entrer dans le vif du sujet il convient de bien connaitre son cube et d'établir quelques règles afin de s'assurer que nous parlerons bien des mêmes choses tout au long de ce guide.

Les différents blocs

Un Rubik's Cube est composé de 26 blocs que l'on peut classer en trois catégories:

Les centres. Ce sont les blocs situés au centre de chaque face, ils sont donc au nombre de six et, contrairement à tous les autres, ont la particularité de ne jamais changer de place. Nous le vérifierons d'ici peu quand nous aborderons les couleurs. Ces blocs ne présentent qu'une seule face visible.

Les arêtes. Elles présentent deux faces visibles. Chaque arête peut être positionnée à la place de n'importe quel autre arête et avec une orientation différente.

Les coins. Dernier cas de notre cube, les coins présentent trois faces visibles et comme les arêtes, ils peuvent se positionner à la place de n'importe quel autre coin et selon une orientation différente.

Le code couleur

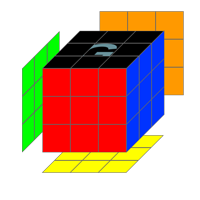La plupart des Rubik's cube reprennent le même code couleur à l’exception de la face noire qui peut être blanche, cette dernière affiche généralement le logo du fabriquant sur le bloc central. J'utiliserais tout au long de ce tutoriel le noir pour représenter cette face.

Comme je l'ai mentionné plus haut, les blocs centraux ne se déplacent pas, du moins ils ne se déplacent pas par rapport aux autres. Vous aurez beau triturer votre cube dans tous les sens, ce sont les coins et les arêtes qui se déplacent, jamais les centres. Et je vous le prouve. Orientez votre cube tel que l'image ci-contre et repérez le centre rouge de votre cube; il aura toujours comme voisin de droite le centre bleu, comme voisin de gauche le centre vert, comme voisin du bas le centre jaune, comme voisin opposé le centre orange et bien sûr comme voisin du haut le centre noir.

Voila qui est dit. Ces quelques explications vous paraissent peut être superflues mais vous verrez par la suite que nous allons sans arrêt nous repérer à la couleur des centres pour reconstruire notre cube.

Si à l'avenir je vous parle par exemple de pivoter "la face verte", comprenez bien que la face en question n'est pas nécessairement remplie de vert mais qu'il s'agit simplement de pivoter la face dont le centre est vert, quelque soit la couleur des coins et des arêtes.

Première étape: placer les arêtes et former la croix

Ci-contre voici l'image du dessin que nous souhaitons réaliser sur notre cube. Plus loin dans le tutoriel je vous apprendrais, à l'aide d'un mnémotechnique (la chaise), une combinaison de mouvements permettant de déplacer trois arêtes sans influencer les autres blocs, ceci vous permettra de gagner un peu de temps, mais dans un premier temps je vous invite à le réaliser de manière intuitive et ce plusieurs fois de suite en utilisant le moins de mouvements possible, c'est un bon exercice qui vous familiarisera avec votre cube.

Comme je l'ai déjà dit à deux reprises, les centres ne bougent pas, c'est donc sur les quatre arêtes que nous allons nous focaliser. Commencer par en placer une à coté du centre noir, puis faites pivoter la face noire autour de son axe jusqu'à faire correspondre la face colorée de l'arête avec le centre de la même couleur.
Continuez jusqu'à réaliser une croix semblable à l'image ci-dessus.

Deuxième étape: placer les coins pour former la face noire et sa couronne

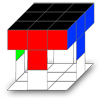Il faut maintenant placer les quatre coins disposant d'une face noire et les orienter pour que leur face colorée corresponde bien avec les centres de même couleur. Vous devriez au final obtenir quelque chose de semblable à l'image ci-contre.

Bien qu'il existe un algorithme pour déplacer trois coins d'un seul coup (le petit canard curieux), je ne vous le recommande pas à ce stade de la reconstruction car même si l'enchaînement est simple le résultat est parfois déroutant. Mais rassurez vous nous en aurons besoin et je vous l'expliquerais en temps voulu. Pour le moment contentez vous de le faire de manière intuitive.

J'ajouterais simplement que:

Les coins dont la face noire est visible sur un coté du cube seront les plus rapide à placer.

Les coins dont la face noire est visible à la base du cube (face jaune dans notre exemple) ou les coins mal placés sur la première couronne devront avant tout être déplacés ce qui vous coûtera quelques mouvements supplémentaire.

Troisième étape: construire la seconde couronne grâce à Mme Tetenlair

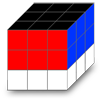À partir de maintenant les choses vont commencer à devenir intéressantes puisque nous allons voir comment déplacer une arête de 45° vers la droite ou la gauche en utilisant un algorithme. Pour nous en souvenir facilement nous utiliserons le mnémotechnique de "Madame Tetenlair". Au final nous obtiendrons une figure semblable à l'image ci-contre.

Dans un premier temps il faut identifier les arêtes à replacer. A ce stade il nous reste 8 arêtes à positionner mais seuls 4 nous intéressent pour réaliser la seconde couronne, les arêtes disposant d'une face jaune sont destinés à la base du cube, on va donc les ignorer.

Le plus simple à mon avis quand vous commencer la seconde couronne consiste à regarder la face jaune pour trouver une arête dont aucune des deux faces n'est jaune (rouge et bleue dans l'exemple). Ceci fait, repositionnez le cube face noire en haut et faites pivoter la face jaune sur son axe jusqu'à aligner l'arête colorée (rouge dans l'exemple) avec la bonne face du cube. Ceci devrait former un grand T de la même couleur tel que l'image ci-dessous.

Pivoter une arête de 45° pour la placer à droite

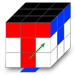Maintenant que vous avez correctement positionné une arête pour former le grand T on peut commencer notre mouvement.

1. Madame Tetenlair voudrait rejoindre ses amies de droite mais elle va à gauche
2. Ces copines viennent la chercher
3. Elle les rejoint
4. Ses copines lui montre le chemin
5. Mais Mme Tetenlair se trompe encore et continue à droite
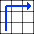6. Dépitée, elle se tourne à droite (là ou elle voulait aller au départ)
7. Fait un pas de côté
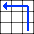8. Et enfin peut rejoindre ses amies.

Pivoter une arête de 45° pour la placer à gauche

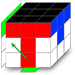Pour placer un coin vers la gauche c'est exactement la même chose mais dans l'autre sens.

1. Madame Tetenlair voudrait rejoindre ses amies de gauche mais elle va à droite
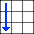2. Ces copines viennent la chercher
3. Elle les rejoint
4. Ses copines lui montre le chemin
5. Mais Mme Tetenlair se trompe encore et continue à gauche
6. Dépitée, elle se tourne à gauche (là ou elle voulait aller au départ)
7. Fait un pas de côté
8. Et enfin peut rejoindre ses amies.

Il arrive souvent qu'une arête soit déjà placée mais mal orientée ou au mauvais endroit. Pas de panique, il faut simplement sortir l'arête mal placée en utilisant l'un ou l'autre des algorithmes que vous venez d'apprendre. Dites vous qu'il faut placer une mauvaise arête (ayant une face jaune) à la place de celle que vous souhaitez récupérer.

Quatrième étape: la croix jaune

Maintenant que vous avez réalisé avec succès la seconde couronne il n'est plus nécessaire de garder la face noire sur le dessus. Pivotez votre cube pour placer la face jaune en haut.
Si vous avez de la chance une croix jaune est déjà dessinée sur cette face, dans ce cas vous pouvez directement passer à l'étape suivante. Si vous n'avez pas de croix, ce qui arrive le plus fréquemment, vous serez confronté à l'un des trois cas suivant:

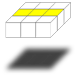1. Facile à identifier, la barre est un alignement qui traverse le cube. Quand vous commencerez l'algorithme qui permet de dessiner la croix, la barre devra être placée horizontalement par rapport à vous comme le montre l'image.

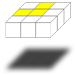2. La virgule ne peut avoir que cette forme. Elle part de l'arête haute, passe par le centre et fini par l'arête gauche. Si ce n'est pas le cas alors ce n'est pas une virgule. Au besoin pivotez l'ensemble du cube sur l'axe noir/jaune pour vous en assurer. Quand vous commencerez l'algorithme qui permet de dessiner la croix, la virgule devra être orientée face à vous tel que le montre l'image.

3. Le dernier cas ne représente aucune des formes attendues. Là encore pas de panique, il suffit de réaliser un des deux algorithmes que vous allez apprendre dans un instant pour qu'une forme apparaisse. Appliquez l'algorithme de la virgule et vous aurez la barre, appliquez celui de la barre et vous aurez la virgule.

Dans les exemples ci-dessus je n'ai représenté que les blocs qui nous intéressent mais d'autre blocs à face jaune peuvent être présents, ainsi cette image représente bien une virgule.

Si la face jaune présente à la fois une virgule et une barre, vérifiez votre double couronne elle est probablement incomplète.

Algorithmes de la virgule et de la barre

Ces enchaînements de mouvements étant très semblables je les présentes l'un au dessus de l'autre.

« Algorithme de la barre

« Algorithme de la virgule

On remarquera que:

• les deux algorithmes commencent et finissent par le même mouvement
• les trois premiers mouvements vont dans le sens des aiguilles d'une montre (on visse)
• les trois derniers mouvements vont dans le sens inverse des aiguilles d'une montre (on dévisse)

Enfin, pour me souvenir sur quelle face appliquer le second mouvement je me dit que si c'est la barre il faut la casser, je visse la face de droite et si c'est la virgule alors je visse la face haute.

À l’exception du cas ou aucune forme n'est dessinée, vous n'aurez pas besoin de réaliser un de ces algorithme plus d'une fois.

Cinquième étape: La croix bien orientée, algorithmes de la chaise

Maintenant que nous avons dessiné la croix sur le dessus du cube il va falloir orienter cette dernière pour que chacune des arêtes corresponde avec la bonne couleur de la face adjacente. Pour y parvenir nous apprendrons deux nouveaux algorithmes très semblables (chaise droite et chaise gauche) qui vous permettront de déplacer trois arêtes à l'exception de celle qui se trouve en face de vous dans le sens horaire ou antihoraire.
Mais avant de commencer je vous propose d'observer les trois cas de figure possible.

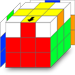1. Une seule arête est correctement positionnée.

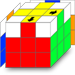2. Deux arêtes côte à côte sont bien positionnées.

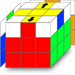3. Deux arêtes face à face sont bien positionnées.

Le cas n°1 est le seul qui permettra à l'algorithme de déplacer les trois arêtes mal positionnées jusqu'à obtenir le résultat souhaité. N'oubliez pas que l'arête bien positionnée doit se trouver face à vous (rouge-jaune dans notre exemple).

Le cas n°2 ne permettra pas à l'algorithme de placer convenablement les trois autres arêtes. En effet, chaque fois que vous le réaliserez vous vous retrouverez dans une situation identique avec deux arêtes bien placées et deux mal placées. Mais la situation n'a rien de dramatique puisqu'il suffit de pivoter la face jaune sur son axe pour faire correspondre une des deux arêtes mal positionnée vers la face adéquate. Vous vous retrouverez alors dans le cas n°1.

Le cas n°3 est celui qui vous coûtera le plus de mouvement (1 algorithme de plus). Pivotez l'ensemble du cube (la face bleue devant vous par exemple) de sorte qu'une arête mal placée se retrouve face à vous. Réalisez un des deux algorithmes de la chaise et vous vous retrouverez alors dans la situation du cas n°1 ou n°2.

Si on fait référence à l'image du cas n°1, on constate que si on fait tourner les arêtes dans le sens horaire il faudra répéter l'algorithme deux fois alors que dans le sens antihoraire une fois suffira.

Déplacer trois arête dans le sens horaire (chaise de droite)

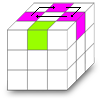Algorithme qui permet de déplacer trois arêtes dans le sens des aiguilles d'une montre à l'exception de celle qui nous fait face. Mnémotechnique de la chaise de droite.

1. Je me lève de la chaise de droite.
2. Je fais 2 pas.
3. 
4. La chaise tombe.
5. Je fais un pas en arrière.
6. Je relève la chaise.
7. Je fais encore un pas en arrière.
8. Je peux m’asseoir.

Déplacer trois arête dans le sens antihoraire (chaise de gauche)

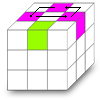Algorithme qui permet de déplacer trois arêtes dans le sens inverse des aiguilles d'une montre à l'exception de celle qui nous fait face. Mnémotechnique de la chaise de gauche.

1. Je me lève de la chaise de gauche.
2. Je fais 2 pas.
3. 
4. La chaise tombe.
5. Je continue d'un pas dans le même sens.
6. Je relève la chaise.
7. Je fais encore un pas dans le même sens.
8. Je peux m’asseoir.

Conclusion sur les algorithmes de la chaise

Quand dans un algorithme on vous demande de faire le même mouvement deux fois de suite, alors peu importe le sens dans le quel on l’effectue. Quand vous tournez une face deux fois à droite, cela revient au même que la tourner deux fois à gauche.

Vous remarquerez que, mis à part la position de la chaise (dans votre esprit), seuls les mouvement de la face jaune du cube diffèrent légèrement. Avec un peu de pratique ces enchaînements vous seront des plus familiers.

J'attire votre attention sur le fait que ce n'est pas la première fois que nous réalisons une croix dont les arêtes doivent être positionnées avec les couleurs correspondantes aux faces adjacentes. Si vous remontez plus avant dans ce tutoriel, vous constaterez que dès la première étape c'est ce que nous avons fait de manière intuitive. N'hésitez pas désormais à utiliser ces algorithmes quand vous commencer la première face du cube.

Sixième étape: Finir le cube

Nous arrivons au terme de notre tutoriel mais la partie est loin d'être gagnée car nous allons avoir de nombreux mouvements à réaliser. Si je résume, notre cube est terminé à l'exception des quatre coins, alors commençons déjà par nous familiariser avec les différents vues que nous propose un coin.

1. Un coin bien placé et bien orienté, facile.
2. Un coin bien placé mais mal orienté.
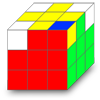3. Un coin mal placé.

Comme pour les arêtes il existe un algorithme qui permet de déplacer trois coins dans le sens horaire ou antihoraire. Le problème avec les coins c'est que quand ils se déplacent, ils en profitent pour pivoter d'un quart de tour ce qui rend leur orientation difficile à anticiper. La première démarche consistera donc à placer les coins au bon endroit peu importe qu'ils soient bien orientés. On utilisera pour cela l'algorithme du petit canard curieux.

Déplacer les coins avec l'algorithme du petit canard curieux

Si vous avez déjà cherché des tutoriels sur le Rubik's Cube il est fort probable que vous ayez entendu parler du mnémotechnique de "Madame Curieuse". L'histoire du "petit canard curieux" est exactement la même à ceci près qu'un canard fait "coin coin" et que c'est bien de cela qu'il s'agit.

Déplacer trois coins dans le sens horaire

Cet enchaînement va déplacer trois coins (rose) dans le sens des aiguilles d'une montre à l'exception du coin (vert) qui se trouve face à vous et à droite.

1. Le petit canard voit monter ses ami de gauche.
2. Il va voir ce qu'ils font.
3. Il voit monter ses amis de droite.
4. Il va voir ce qu'ils font.
5. Il voit ses amis de gauche redescendre.
6. Il va voir ce qu'ils font.
7. Il voit ses amis de droite redescendre.
8. Il va voir ce qu'ils font.

Déplacer trois coins dans le sens antihoraire

Cet enchaînement va déplacer trois coins (rose) dans le sens des inverse des aiguilles d'une montre à l'exception du coin (vert) qui se trouve face à vous et à gauche.

1. Le petit canard voit monter ses ami de droite.
2. Il va voir ce qu'ils font.
3. Il voit monter ses amis de gauche.
4. Il va voir ce qu'ils font.
5. Il voit ses amis de droite redescendre.
6. Il va voir ce qu'ils font.
7. Il voit ses amis de gauche redescendre.
8. Il va voir ce qu'ils font.

Bien orienter les arêtes avec l'algorithme de la double chaise

L'algorithme de la double chaise n'est pas nouveau, il consiste simplement à réaliser l'algorithme de la chaise droite immédiatement suivit de l'algorithme de la chaise gauche.
Je vous rappel que ces algorithmes permettent de déplacer des arêtes, mais ce que vous n'aviez peut-être pas remarqué c'est qu'ils pivotent également des coins.

Le fait d'appliquer une double chaise à cette étape du Rubik's cube aura pour incidence de pivoter les deux coins situés sur la face de droite sans les déplacer et n'affectera en rien les deux coins de la face gauche. Rassurez vous vos arêtes ne bougeront pas non plus.

Maintenant que nous savons cela nous pouvons enfin terminer notre cube. Si vous avez réussi à positionner tous les coins à leur place respective (ce qui doit être le cas) vous devez vous trouver dans l'une des situation suivante:

1. Tous les coins sont mal orientés.
   Depuis n'importe quelle face, vous devrez réaliser au maximum deux double chaises pour vous trouver dans la situation d'un des trois autre cas.

2. Un seul coin est bien placé et bien orienté.
   Orientez le cube de manière à voir le coin bien orienté sur le coté gauche, faites une double chaise pour vous retrouver dans le cas n°3 ou n°4.

3. Deux coins sont bien placés et bien orientés du même coté.
   Orientez le cube de manière à voir les deux coins bien orientés du coté gauche, les deux coins mal orientés bien visibles du coté droit. Vous ne devriez pas avoir plus de deux double chaises à réaliser pour finir le cube. Félicitation!

4. Deux coins sont bien placés et bien orientés en diagonale.
   Depuis n'importe quelle face effectuez une double chaise, vous vous trouverez alors dans le cas n°3. Orientez le cube de manière à voir les deux coins mal orientés bien visibles du coté droit. Une seule double chaise devrait vous permettre de finir le cube. Félicitation!

Conclusion

Alors vous voyez ce n'était pas si difficile, vous allez enfin pouvoir replacer votre Rubick's cube bien en évidence sur son étagère, mais désormais ce ne sera plus cet objet multicolore qui par sa seule présence vous montrait du doigt et criait: Houuuu. Bien sûr vous allez devoir vous entraîner avant d'épater la galerie mais je gage que vous aurez votre petit succès chaque fois que vous serez invité quelque part et que vous verrez un Rubik's cube servir de presse-papier.

BONUS: Pivoter une arête bien placée mais mal orientée

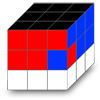Quand on cherche à finir la seconde couronne il n'est pas rare qu'une arête soit bien placée mais mal orientée. La méthode utilisée dans ce tutoriel consiste à utiliser l'algorithme de "Madame Tetenlair" à deux reprises. Il existe néanmoins un algorithme qui permet de le faire en une seule fois et de gagner un peu de temps. Pour nous aider à le retenir j'ai concocté le mnémotechnique de la nouvelle pair de chaussures.

L'algorithme de la nouvelle pair de chaussures.

1. Je regarde mes pieds.
2. Je fais un pas (dans le sens de l'arête à déplacer).
3. Je relève la tête.
4. Je fais deux pas.
5. 
6. Je regarde mes pieds.
7. Je fais deux pas.
8. 
9. Je relève la tête
10. Je fais un pas vers la chaise (dans le sens de l'arête à déplacer).
11. Je m’assois.
12. Je quitte les chaussures.
13. Je me relève.

BONUS: Pivoter deux coins bien placée mais mal orientée

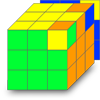
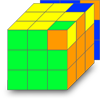Quand on arrive à la fin de notre puzzle on se retrouve irrémédiablement dans l'une de ces deux positions, deux coins bien placés mais mal orientés. On peut rapidement identifier la différence entre ces deux image grâce aux deux faces jaune. Dans l'image de gauche elles sont sur deux faces opposées du Rubik's cube alors que sur l'image de droite elles sont sur la même face. Ce détail n'est pas sans importance. Si vous avez suivi mon tutoriel vous savez résoudre le problème en utilisant le double algorithme de la chaise. Ce que vous n'avez peut-être pas remarqué c'est que quand vous êtes dans le cas de l'image de droite (deux faces jaune du même coté) il suffit de réaliser une seule "double chaise" pour finir le cube sois 16 mouvements, alors que dans le cas de l'image de gauche vous devrez réaliser deux fois l'algorithme de la "double chaise" pour finir le cube sois 32 mouvements.

Algorithme de Fab et mnémotechnique du courant d'air

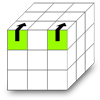L'algorithme de Fab permet de basculer les deux faces de même couleur et du même coté sur la face voisine du cube en 16 mouvements. Il faudra pour cela positionner le cube de sorte que les deux même couleurs soient face à nous. Vous avez compris que dans le cas de l'image ci-dessus à droite on ne gagne rien sinon d'apprendre un algorithme de plus, mais dans le cas de l'image ci-dessus à gauche on gagne quand même 16 mouvements, on va pas cracher dans la soupe. En plus je vous ai concocté un mnémotechnique qui tient la route.

1. Je pose le papier sur la table.
2. Je vais vers la fenêtre.
3. Le papier s'envole.
4. Je reviens vers la table.
5. Je pose le papier sur la table.
6. Je vais vers la fenêtre.
7. Le papier s'envole.
8. Je le rattrape de justesse.
9. Je ferme la fenêtre.
10. Je vais vers table.
11. La fenêtre s'ouvre.
12. je vais vers la fenêtre.
13. Je la ferme.
14. Je vais vers la table.
15. La fenêtre s'ouvre.
16. Tant pis je sors.

Astuce

Pour vous entraîner à réaliser cet algorithme faites celui de la double chaise depuis un cube fini. Vous vous retrouverez devant le cas de figure adéquate.

manu gogolplex.org

^